排序算法

定义

将一组杂乱无章的数据按一定的规律次序排列起来

目的

便于查找

如何衡量排序算法好坏

时间效率

排序速度，即排序所花费的全部比较次数

空间效率

占内存辅助空间的大小

稳定性

若两个记录A和B的关键字值相等，但排序后A、B的先后次序保持不变，则称这种排序算法是稳定的

两种方式

内部排序--在内存排序 外部排序--在外部的存储排序

四种排序方法

插入排序

直接插入排序

• 先将序列中第1个记录看成一个有序子序列，然后从第2个记录开始，逐个插入，直至整个序列有序，排序过程为 n-1 趟插入
• 时间复杂度： O（n的平方）
• 空间效率： O（1）
• 算法稳定性：稳定

希尔排序

• 先取一个正整数 d1<n，把所有相隔 d1 的记录放为一组，组内进行直接排序；然后取 d2<d1，重复上述分组和排序操作；直至 di=1，即所有记录放进一个组中排序未知
• 一般取 d1=n/2，d（i+1）=di/2，如果结果为偶数，则加1
• 算法稳定性：不稳定

选择排序（前提：顺序存储结构）

直接选择排序（简单选择排序）

在所有记录中选出最小的记录，把它与第1个记录交换，然后剩余的记录内选出最小的记录与第2个交换，依次类推

堆排序

• 堆
  • 堆是满足虾类性质的数列{r1，r2，......r n}
  • 若 ri <= r2i 或 ri <= r（2i+1），则为小顶堆 --孩子的权值要比父亲的权值大，根节点是权值最小的元素
  • 若 ri >= r2i 或 ri >= r（2i+1），则为大顶堆 --父亲的权值要比孩子的权值大，根节点是权值最大的元素
  • 若将该数列视作完全二叉树，则 r2i是ri 的左孩子，r（2i+1）是 ri 的右孩子
• 堆排序即是利用堆的特性对记录序列进行排序的一种排序方法
• 将无序序列建成一个堆，得到关键字最小（或最大）的记录；输出堆顶的最小（大）值后，是剩余的 n-1 个元素又建成一个堆，则可得到 n 个元素的次小值；重复执行，得到一个有序序列，这个过程为堆排序
• 输出堆顶元素之后，以堆中最后一个元素替代之；然后将根节点值与左右子树的根节点值进行比较，并与其中小者进行交换；重复上述步骤，直至叶子结点，将得到新的堆，称这个从堆顶至叶子的调整过程为“筛选”
• 时间复杂度： O（nlog2n）
• 空间效率： O（1）
• 算法稳定性：不稳定

交换排序

冒泡排序

• 基本思路
  • 每趟不断将记录两两比较，并按“前小后大”（或“前大后小”）规则交换
• 最好情况 -初始排列已经有序，只执行一趟起泡，做 n-1 次关键码比较，不移动对象
• 最坏情况
  • 初始排列逆序，要执行 n-1 趟起泡
• 时间复杂度： O（n的平方）
• 空间效率： O（1）
• 算法稳定性：稳定

快速排序（前提：顺序存储结构）

• 采用分治法的算法策略
• 从待排序列中任取一个元素（一般取第一个元素）作为中心，所有比它小（或相等）的元- 素一律放前，所有比它大的元素一律放后，形成左右两个子表；
• 然后再对各子表重新选择中心元素并按此规则调整，直到每个子表的元素只剩一个。此时- 便为有序序列。
• 最坏的时间复杂度为 O（n的平方）
• 最好的时间复杂度为 O（nlog2n）
• 空间效率： O（1）
• 算法稳定性：不稳定

归并排序

• 可以把一个长度为 n 的无需序列看成是 n 个长度为 1 的有序子序列，首先做两两归并，得到 n/2 个长度为 2的有序子序列；再做两两归并，如此重复，直到最后得到一个长度为 n 的有序序列
• 时间复杂度： O（nlog2n）
• 空间效率： O（n）
• 算法稳定性：稳定

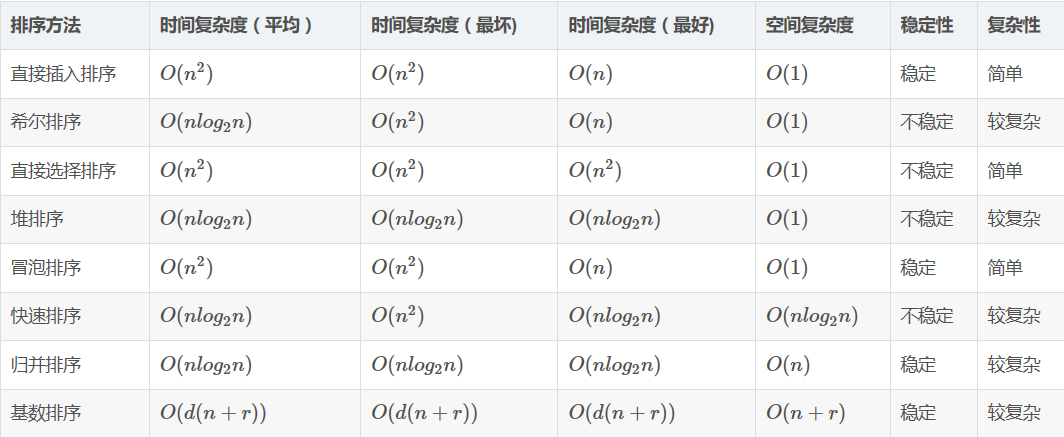
常见排序算法及对应的时间复杂度和空间复杂度